Современные тренды в научно-образовательной сфере заставляют высшие учебные заведения пересматривать свои целевые модели и стратегии развития. И одна из основных задач в этом направлении – обеспечить организацию и ведение образовательной деятельности в вузах на мировом уровне, позиционировать отечественные университеты не только как узнаваемые, но и признаваемые за рубежом. Наличие современных образовательных программ и современной материально-технической базы в вузах – необходимое, но недостаточное условие их вхождения в число ведущих университетов мира. По мнению авторов, основополагающим фактором повышения престижности и конкурентоспособности вузов на мировом рынке является глобализация и интернационализация их образовательных услуг и сервисов. И здесь важно всё: интернационализация основных образовательных программ, экспорт/импорт образовательных услуг, академическая мобильность не только студентов, но и преподавателей, развитые информационно-телекоммуникационные технологии, формирование международных стандартов образовательных программ, гармонизированных не только со стандартами ведущих мировых держав, а также многое другое.
В международной системе высшего образования, безусловно, есть лидеры в построении стратегии и концепции интернационализации рынка образовательных услуг (американская модель, британская модель, немецкая модель). Но парадокс заключается в том, что практически все страны выстраивают собственные национальные образовательные системы, активно используя при этом обучение своих студентов за рубежом. Не вдаваясь в анализ этого феномена (здесь много аспектов: и политических, и национальных, и экономических и т.д., вплоть до социально-гуманитарных), отметим безусловную важность и полезность обучения иностранных студентов и для принимающей страны, так как не бывает бесполезных коммуникаций. Любые коммуникации расширяют кругозор всех участников образовательного процесса и взаимно повышают их культуру, в том числе и научную.
Основная проблема обучения иностранных студентов – это изучение различных дисциплин на неродном для студентов языке в неродной социокультурной среде. В связи с этим необходимо постоянно искать новые инновационные методы достижения главной цели высшего профессионального образования – формирование у студентов знаний, навыков, практических умений и использование их в различных видах деятельности.
В настоящей работе авторами на основе опыта проведения занятий с иностранными студентами в Национальном исследовательском Томском политехническом университете (ТПУ) проведен анализ – по каким причинам не удаётся сформировать необходимые компетенции иностранных студентов при изучении математического цикла дисциплин, а также, каким образом эти причины, возможно, могут быть устранены.
Одной из основных причин, по мнению авторов, является то, что некоторая часть предлагаемой по дисциплине информации до иностранных студентов не доходит. И это в первую очередь связано с плохим слуховым восприятием информации. Большая часть иностранных студентов с трудом воспринимает слова лектора или преподавателя, ведущего практику. Насколько бы ни был преподавателем доступно изложен материал, эффективность усвоения резко падает, если возникают трудности с пониманием этнического языка принимающей страны (в данном случае – русского языка). Понятно, что всего лишь за один год предвузовской подготовки (именно такая практика принята в ТПУ) иностранным студентам сложно овладеть неродным языком (русским) до «уверенного» уровня, поэтому подобные проблемы возникали и будут возникать постоянно.
Что можно сделать хотя бы для частичного устранения этой проблемы? Прежде всего, отметим, что в ТПУ иностранные студенты имеют возможность первые два года обучаться отдельно от остальных студентов, что существенно помогает повысить их уровень «уверенного» владения русским языком. Преподаватели могут излагать материал на адаптированном для иностранных студентов языке, используя более простые фразеологические обороты, несколько замедленный темп речи и тому подобное, что невозможно при совместном обучении и иностранных и русских студентов. Так как в основных образовательных программах изучение математических дисциплин происходит именно в первые два года обучения, то данное преимущество является достаточно весомой составляющей для успешного формирования универсальных и профессиональных компетенций.
Понимая, что зрительное восприятие информации обычно бывает гораздо более развито, чем слуховое, изложение учебного материала можно сопровождать «усиленным» визуальным рядом. Особенно это характерно для математических текстов, которые в силу своей специфики содержат огромное количество формул. Правда стоить отметить и особенность математических текстов – во многих случаях они имеют одинаковую запись на любых языках. Но и математической нотации тоже надо учить.
В ТПУ имеются все возможности для использования в процессе обучения аудио и видеорядов демонстрационных материалов. Большая часть аудиторий снабжена современным мультимедийным оборудованием, которое может использоваться как на лекционных, так и на практических занятиях. Использование уникальных авторских презентаций при чтении лекций по дисциплинам «Линейная алгебра и аналитическая геометрия» и «Математический анализ» показало, что значительно увеличивается скорость подачи материала и улучшается понимание иностранными студентами предмета. Практические занятия также сопровождаются соответствующим авторским дидактическим материалом, который позволяет иностранным студентам легче ориентироваться по их тематике.
Следует обратить внимание, по мнению авторов, и на то, что порой имеет место элементарное недостаточно хорошее усвоение фактического материала иностранными студентами, что приводит, естественно, к некачественному владению необходимыми навыками и умениями. И причина здесь не в преподавателях. Это обусловлено, в первую очередь, постоянно уменьшающимся количеством аудиторных часов, отводимых на дисциплину, достаточно высоким и интенсивным темпом обучения (есть требования Рабочей программы дисциплины), а также отсутствием у иностранных студентов необходимых базовых знаний, которые позволили бы им успешно овладевать новой информацией.
У каждого преподавателя, конечно, имеются в арсенале свои способы и методы «подтягивания» отстающих студентов. Но хотелось бы отметить следующий момент. В ТПУ начала своё действие трёхуровневая система подготовки студентов, при которой для слабо подготовленных студентов еженедельно проводятся дополнительные занятия. На таких адаптационных курсах студенты, не успевающие усвоить материал вместе с остальными, могут разобрать непонятые моменты отдельно с преподавателем и в более медленном темпе. Эффективность таких занятий была наглядно продемонстрирована после проведения контролирующих мероприятий у иностранных студентов первого курса нашего университета, изучающих одновременно две математические дисциплины: «Линейная алгебра и аналитическая геометрия» и «Математический анализ». В рамках дисциплины «Математический анализ» такого рода адаптационный курс был предусмотрен и проводился на протяжении первых восьми недель обучения. По дисциплине «Линейная алгебра и аналитическая геометрия» дополнительные часы на этот курс не были выделены. Результаты показали, что итоги усвоения обеих дисциплин у неотстающих студентов были примерно одинаковые, а вот «слабые» студенты гораздо лучше справились с контролирующими мероприятиями по дисциплине «Математический анализ», чем по дисциплине «Линейная алгебра и аналитическая геометрия», что, несомненно, объясняется дополнительной работой этих студентов во время адаптационного курса.
В связи с дополнительными занятиями с иностранными студентами, отметим и необходимость повышения уровня профессионально-коммуникативных компетенций и самих преподавателей во владении иностранным языком. Но здесь важна мотивация преподавателей в совершенствовании своей языковой подготовки, а в перспективе – и мотивация формирования функционального многоязычия. Но такую мотивацию обеспечить без административного ресурса весьма проблематично.
Еще одним из способов устранения вышеуказанных проблем может быть применение метода аналогии в процессе обучения иностранных студентов, особенно математическим дисциплинам, так как в основе решения проблем математики всегда есть построение разнообразных абстрактных структур и классов, выявление тождественности, подобия и связи между ними или их элементами. Аналогия – основной инструмент и самой математики.
Общепринятым фактом является и то, что процесс изучения любой науки значительно основывается на переносе свойств и отношений из одной системы в другую, что также приводит к применению такого метода научного познания, как метод аналогии. Умение переносить знания, полученные при изучении одного объекта, на другие – это одна из главных задач, как развития науки, так и образования, откуда следует, что формирование у иностранных студентов умения думать аналогиями, применять методы аналогии в познании можно рассматривать как один из эффективных путей повышения качества образования иностранных студентов [3].
Под методом аналогии в обучении математике будем понимать такой метод обучения, при котором обоснованно и целенаправленно устанавливаются связи между различными её разделами. Будем придерживаться определения понятия математической аналогии, данного Е.А. Беляевым: «Математическая аналогия есть тождественность в широком смысле каких-либо систем математических объектов, возникающая как результат совмещения данных систем и основывающаяся на внутреннем сходстве и взаимосвязанности математики в целом» [1].
Выделим такой вид аналогии как аналогия применения. Если заданы внешне разнородные системы объектов произвольной природы и в них глубоко заложено сходство и есть возможность применить к ним один и тот же математический аппарат, то в этом случае говорят об аналогии применения.
С помощью аналогии применения иностранные студенты смогут изучать одно из фундаментальных понятий современной математики – линейные неравенства, а также их связи с геометрическими объектами [2]. При этом изложение теоретического материала сопровождается соответствующими задачами, с их помощью вводятся и изучаются базовые математические понятия, которые связаны с понятиями выпуклых множеств, плоскости, пространства и др.
Геометрическую фигуру можно рассматривать как множество точек плоскости или пространства, из которых она состоит. Задать фигуру – значит записать соотношения между координатами этих точек, с помощью которых можно определить, принадлежит та или иная точка этой фигуре или нет. Например, используя метод аналогии, можно показать, что системы линейных неравенств с двумя неизвестными описывают выпуклые многоугольники, а с тремя неизвестными – выпуклые многогранники [4]. Таким образом, выпуклый многоугольник (многогранник) всегда можно задать аналитически, системой линейных неравенств. Если рассмотреть параллелепипед, у которого длины сторон соответственно равны 3, 5, 4, то он задаётся следующей системой линейных неравенств: ![]()
Такая геометрическая интерпретация помогает иностранным студентам быстрее запомнить и осмыслить понятия плоскости, пространства, познакомить их с геометрическим методом решения [5].
Геометрическое решение систем линейных неравенств с двумя и тремя неизвестными играет важную роль не только в общеобразовательном аспекте изучения свойств пространства, геометрического представления фигур, развития аналитического и образного мышления, но и является основой построения выпуклых множеств, решения систем линейных неравенств в линейном программировании, т.е. занимает немаловажное место в прикладной, современной направленности обучения геометрии.
Ниже в целях иллюстрации приведены примеры задач, которые при соответствующей геометрической интерпретации достаточно хорошо усваиваются студентами, причём не обязательно владеющими русским языком на «уверенном» уровне.
1. Запишите систему линейных неравенств, выражающую тетраэдр, вершина которого лежит в начале системы координат, а все ее боковые ребра лежат на координатных осях и равны 3 см.
2. Найдите все пары целых чисел, удовлетворяющих неравенствам: 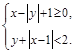
3. Задайте с помощью неравенств многоугольники, у которых вершинами являются: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
Таким образом, можно сделать вывод, что использование аналогии применения, в частности, использование идей и методов аналитического представления разнообразных геометрических фигур, дает преподавателю большие возможности для оживления и обогащения курса математики, что особенно важно для иностранных студентов, а также формирует у студентов ощущение единства математики. А мысленное представление изменяющихся фигур или их элементов положительно сказывается на развитии пространственного и аналитического мышления обучаемых.
Рецензенты:
Рожкова С.В., д.ф.-м.н., профессор кафедры организации и технологии высшего профессионального образования ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет», г. Томск.
Тартаковский В.А., д.ф.-м.н., зав. лабораторией Института мониторинга климатических и экологических систем СО РАН, г. Томск
Библиографическая ссылка
Шерстнёва А.И., Янущик О.В., Пахомова Е.Г. АНАЛОГИЯ ПРИМЕНЕНИЯ КАК СРЕДСТВО ПОВЫШЕНИЯ УРОВНЯ ОБЩИХ КОМПЕТЕНЦИЙ ИНОСТРАННЫХ СТУДЕНТОВ // Современные проблемы науки и образования. 2013. № 6. ;URL: https://science-education.ru/ru/article/view?id=11052 (дата обращения: 27.04.2025).



