Для построения методики исследования процесса резания порубочных остатков дисковой рубительной машиной [1; 7], оснащенной различными типами ножей, полагаем, что порубочные остатки, которые измельчаются режущими элементами, представляют собой сплошную среду с заданными характеристиками и свойствами. При этом режущий элемент (нож) может иметь различную форму:
- с тремя лезвиями, расположенными ступенчато и заданными геометрическими параметрами (рисунок 1) [2];
- с одним лезвием и заданными геометрическими параметрами (рисунок 2).
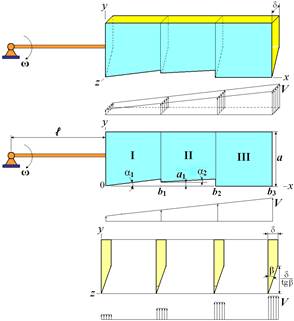
Рисунок 1 - Режущий элемент с тремя лезвиями, расположенными ступенчато - комбинированный нож
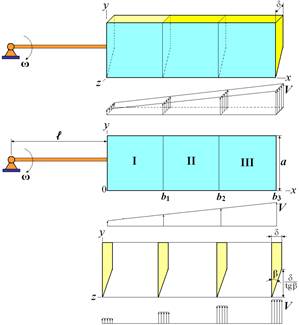
Рисунок 2 - Режущий элемент с одним лезвием (традиционный нож)
Для создания острых режущих кромок ножей на участках 0 ≤ x ≤ b3 выполнен срез в плоскости yz под углом β (рисунки 1, 2). Для эффективного резания угол β выбирается максимально острым, но при этом должно быть выполнено соотношение δ/tgβ < α.
Для режущих элементов с тремя лезвиями (рисунок 1) углы α1, α2 должны быть невелики, например <30°, и углубление ступенчатых вырезов в тело ножа при 0 ≤ x ≤ b2 также должно быть небольшим. Это необходимо, чтобы режущие кромки ножа, определяемые ступеньками b1 tgα1 и (b2-b1) tgα1 при 0 ≤ x ≤ b1 и b1 ≤ x ≤ b2 , были достаточно острыми.
При больших углах α1, α2 и при большом углублении ступенчатых вырезов в тело ножа при 0 ≤ x ≤ b2 в плоскости xz возникают плоские треугольные и трапецеидальные площадки (рис. 3а), и процесс резания становится неэффективным. Заострить комбинированный нож под одни углом β на всех его участках можно, например, вырезав ступенчатые площадки на задней поверхности ножа, как показано на рисунке 3б.
а)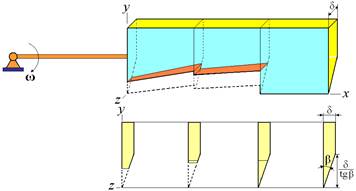
б)
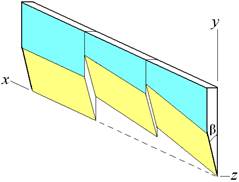
Рисунок 3 - Возможные неэффективная (а) и эффективная (б) формы ножа с тремя лезвиями
Режущие элементы расположены по периферии измельчителя, выполненного в виде плоского диска, например, как показано на рисунке 4.
В процессе математического моделирования будут получены следующие результаты.
· Для двух ножей: комбинированный из трех лезвий (рисунок 1) и традиционный (рисунок 2) должны быть построены математические модели, описывающие процессы резания порубочных остатков и включающие в себя следующее.
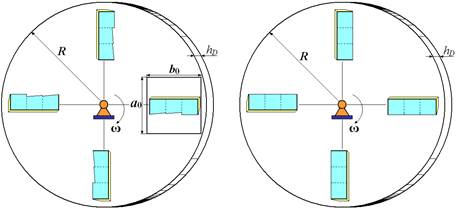
Рисунок 4 - Расположение на диске режущих элементов с тремя и одним лезвием
- Аналитические выражения для главного вектора и главного момента сил сопротивления (в том числе сил и моментов сопротивления резанию) и их составляющих в трехмерном пространстве, как функции геометрических и физических параметров и характеристик ножей на всех участках I, II, III и характеристик сплошной среды порубочных остатков, параметров движения ножа:
, 
.
, 
,
где 
- геометрические параметры; ρ – плотность среды; ω – угловая скорость вращения.
- Аналитические выражения для главного вектора и главного момента сил вязкого трения, как функции геометрических и физических параметров и характеристик ножей на всех участках I, II, III и сплошной среды порубочных остатков, параметров движения ножа.
, 
,
, 
,
где μ – динамическая вязкость среды.
- Аналитические выражения для главного вектора и главного момента сил сухого трения, как функции скорости 
потока рассматриваемой сплошной среды относительно ножа.
, 
.
где ε – коэффициент сухого трения.
- Для двух ножей (рисунки 1 и 2) должен быть проведен качественный сравнительный анализ полученных характеристик процесса резания.
- Должны быть получены и исследованы динамические уравнения вращательного движения диска с ножами, получены формулы для оценки мощности сил сопротивления при процессе резания порубочных остатков.
- Для двух ножей (рисунки 1 и 2) должен быть разработан программный комплекс, реализующий построенные математические модели и позволяющий проводить автоматизированные расчеты рассматриваемых параметров процесса резания при задании исходных данных.
- Должна быть проверена работоспособность построенных математических моделей и разработанного программного обеспечения путем проведения компьютерных экспериментов и сравнения процессов резания двумя ножами (рисунки 1 и 2), в том числе по энергетическим характеристикам.
- Должна быть учтена подача порубочных остатков в зону резания и производительность процесса резания.
При составлении методики исследований предусматривался общий подход к построению математических моделей процессов переработки древесины в щепу и для расчетов и оптимизации сил и моментов сил резания.
При вращательном движении диска, для каждого режущего элемента (ножа), в рассматриваемой сплошной среде (рисунки 1, 2, 4) справедливо уравнение вращательного движения [3; 4]:
, (1)
где J – момент инерции режущего элемента относительно оси вращения, ω – угловая скорость вращения, Mвр – вращательный момент привода, 
– суммарный момент сил сопротивления.
В суммарном моменте сил сопротивления учитываются силы и моменты режущих сил (по оси y), силы и моменты сил вязкого и сухого трения.
Полагается, что привод достаточно мощный и его вращательный момент уравновешивает суммарный момент сил сопротивления.
При выполнении M = ΣMC угловая скорость вращения ω = ω0 = const.
Для оценки энергетических затрат используется формула [5] для мощности внешних сил ME, действующих на вращающийся с угловой скоростью ω диск с ножами:
. (2)
Процесс резания рассматривается как вращательное движение режущего элемента (ножа) заданной геометрической конфигурации с учетом сил сопротивления в рассматриваемой сплошной среде.
Полагается, что поток рассматриваемой сплошной среды совершает движение относительно ножа с заданной эпюрой скоростей (рисунки 1, 2):
. (3)
Этот поток сплошной среды имеет заданную площадь поперечного сечения S = b·δ, где b, δ размеры прямоугольного поперечного сечения, соответствующие геометрическим характеристикам ножа, и ударяется под заданным углом γ о площадку AB режущего элемента с нормалью 
(рисунок 5).
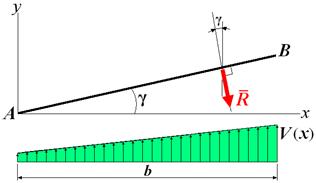
Рисунок 5 - Схема к определению силы давления R
При этих данных необходимо определить силу давления , производимого сплошной средой на поверхность режущего элемента.
Это и будет основной составляющей сил сопротивления, т.е. сил давления и резания.
Для решения поставленной задачи применим теорему импульсов [6] к движению объема сплошной среды за некоторый промежуток времени τ.
Этот объем заполняет участок сплошной среды длиной V(x)·τ и площадью S = b·δ.
Масса этого объема:
, (4)
где ρ – плотность сплошной среды.
На рассматриваемую систему действует сила реакции ножа , направленная перпендикулярно режущей поверхности ножа AB (рисунок 4). Другие силы в такой постановке, в силу их малости по сравнению с , на данном этапе не учитываются.
Воспользуемся теоремой импульсов в проекции на направление вектора , формулировка и математическое представление которой имеют следующий вид.
Изменение проекции количества движения механической системы на любую ось равно сумме проекций на ту же ось импульсов всех внешних сил, действующих на систему:
, (5)
Количество движения рассматриваемого объема сплошной среды в момент времени t1 = 0 является вектором, имеющим направление скорости V и модуль
.
Его проекция на направление (рисунок 5):
. (6)
К моменту времени t2 = τ частицы сплошной среды, без учета «брызг» отдельных фрагментов, приобретут скорости, направленные по поверхности AB (рисунок 5).
Тогда проекция количества движения рассматриваемого объема сплошной среды на направление в момент времени t2 = τ:
. (7)
В правую часть (5) входит лишь проекция импульса силы
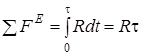. (8)
Подставляя выражения (6), (7), (8) в (5), получим:
.
Отсюда основная формула для модуля сил реакции поверхности, режущего сплошную среду элемента, примет вид:
. (9)
Рецензенты:
Маштаков Д.А., д.с.-х.н., доцент, заведующий кафедрой «Лесное хозяйство и лесомелиорация», ФГБОУ ВПО «Саратовский государственный аграрный университет им. Н.И. Вавилова», г. Саратов.
Панкратов В.М., д.т.н., профессор, заместитель директора, Институт проблем точной механики и управления РАН, г. Саратов.
Библиографическая ссылка
Березников С.В., Фокин С.В. О МЕТОДИКЕ ИССЛЕДОВАНИЯ ПРОЦЕССА РЕЗАНИЯ ПОРУБОЧНЫХ ОСТАТКОВ ДИСКОВОЙ РУБИТЕЛЬНОЙ МАШИНОЙ, ОСНАЩЕННОЙ РАЗЛИЧНЫМИ ТИПАМИ НОЖЕЙ // Современные проблемы науки и образования. – 2013. – № 5. ;URL: https://science-education.ru/ru/article/view?id=10346 (дата обращения: 13.11.2024).