Введение
Задача планирования работ по портфелю проектов относится к классу многокритериальных задач управления сложными системами, время поиска решений которых растет экспоненциально в зависимости от размерности задачи. Классические методы решения задачи планирования обладают рядом недостатков. Так, применение комбинаторных методов, а также математического программирования связано с длительностью вычислений при исследовании задач большой размерности. Кроме того, данные методы испытывают затруднения в поиске оптимума при наличии динамической системы ограничений, меняющейся на каждом шаге планирования [4]. Использование имитационного моделирования позволяет учитывать динамический характер задачи, однако, поиск на основе данного метода носит случайный характер и не гарантирует нахождения оптимального решения. Применение генетической оптимизации позволяет преодолеть выделенные недостатки предыдущих методов, в том числе достичь снижения длительности поиска решения до квадратичной зависимости от размерности задачи [7].
Постановка задачи планирования проектных работ
В общем виде задача планирования работ формулируется как задача определения такой последовательности работ, которая удовлетворяла бы установленным ограничениям и сводила бы к минимуму время выполнения всех работ. В [7] выделено четыре типа ограничений, накладываемых на формируемый план работ: ресурсное, предшествования, физического размещения, информационное. С учетом анализа деятельности проектных организаций целесообразно добавить к данному списку временнóе ограничение, связанное с наличием временных рамок раннего и позднего начала работ по проекту.
В различных исследованиях в зависимости от конкретных решаемых задач рассматриваются различные наборы ограничений при проведении планирования. Так, в [7] учитываются все приведенные ограничения, за исключением временнóго. В исследованиях [4–5] рассматриваются ограничения предшествования и ресурсное. Планирование без учета ограничений представлено в работах [3,6] при определении маршрута движения общественного транспорта и планировании работы производственного участка.
Объекты оптимизации также различаются в рассмотренных исследованиях. Классическая целевая функция задачи планирования по минимизации времени выполнения работ применяется в исследованиях [5–7]. В работах [3-4] в качестве целевой функции выступает суммарное время отклонений выполнения работ от плановых сроков.
Ни в одном из приведенных выше исследований не рассматривается оптимизация привлекаемых субподрядных работ, в то время как данная задача встает перед всеми проектными организациями и даже перед предприятиями с серийным производством. Рассмотрим деятельность проектной организации и сформулируем задачу календарного планирования портфеля проектов с учетом привлечения субподрядных работ.
Введем обозначение периода планирования: 
, где 
– момент времени на интервале планирования; 
– длительность периода планирования. Дано множество проектов портфеля: 
, 
, где 
– i-тый проект портфеля; 
– количество проектов портфеля. Множество операций в проектах: 
, 
, 
, где 
– j-ая операция i-го проекта; 
– количество операций в портфеле проектов.
Введем описание трудовых ресурсов, необходимых для выполнения работ. Множество трудовых ресурсов, имеющихся на предприятии: 
, 
, где 
– количество человек в отделе w; 
– количество отделов на предприятии. Множество трудовых ресурсов субподрядных организаций примем бесконечно большим в том смысле, что при необходимости выделенный объем стороннего ресурса всегда будет найден путем привлечения, если потребуется, нескольких профильных организаций. Данное обстоятельство снимает ресурсное ограничение планирования при решении задачи.
Множество трудовых ресурсов, необходимых для выполнения операций каждого проекта портфеля: 
, где 
– количество трудового ресурса отдела w для выполнения операции. Множество длительностей операций портфеля проектов: 
, множество стоимостей выполнения операций в день: 
.
Множество временных ограничений начал выполнения операций проектов: 
, где 
– дата раннего начала выполнения j-ой операции i-го проекта; 
– дата позднего начала выполнения j-ой операции i-го проекта. В данное ограничение лицом, принимающим решения (ЛПР), включаются ограничение предшествования и информационное ограничение в случае их появления для каких-либо операций портфеля проектов.
Ограничение физического размещения в данной задаче не рассматривается, поскольку работы в рамках проектной деятельности носят либо интеллектуальный характер, либо проводятся на различных территориях заказчиков.
Опишем управляемые параметры рассматриваемой задачи – множество моментов начал выполнения операций: 
. Для решения задачи календарного планирования могут быть использованы следующие критерии оптимизации:
1) Минимизация суммарной стоимости субподрядных работ:
, (1)
где 
– объем субподрядных работ j-ой операции i-го проекта.
2) Минимизация общего простоя отделов предприятия:
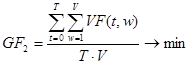, (2)
где 
– количество свободных ресурсов отдела w предприятия в момент t.
Рассмотрим следующую целевую функцию (ЦФ) GF, учитывающую оба выделенных критерия оптимизации решения задачи планирования:
, (3)
где 
– весовые коэффициенты, 
;
– начальные значения целевых функций, полученные путем экспертной оценки ЛПР дат начала операций.
Программный комплекс мультиагентной генетической оптимизации
Рассмотрим оптимизацию решения задачи планирования проектных работ на основе генетического алгоритма (ГА) и мультиагентного моделирования. Методика использования ГА включает в себя выполнение следующих шагов: 1) выбор способа кодирования решения задачи (фенотипа) в особь-хромосому (генотип); 2) определение метода оценки функции пригодности (ФП) решения; 3) описание генетических операторов (ГО); 4) определение законов выживания решения; 5) генерация начальной популяции и работа ГА.
В литературе [3–7] описаны различные способы расчета ФП особей популяции: аналитические методы, имитационное моделирование, искусственные нейронные сети, нечеткие системы, компонентное моделирование. При решении задач планирования работ с ресурсными ограничениями в исследованиях [4–5,7] предпочтение отдается аналитическим расчетам ФП решений. Недостаток подобного подхода заключается в отсутствии учета динамического характера поведения сложной системы. Данный недостаток преодолевается при использовании имитационной модели (ИМ) для оценки ФП решения [3,6]. Кроме того, интеграция эволюционного и имитационного моделирования позволяет ограничить пространство случайного поиска и усилить эвристическую оптимизацию за счет учета динамически меняющихся ограничений задачи планирования.
Для решения задачи интеграции методов эволюционного и имитационного мультиагентного моделирования был разработан программный комплекс (ПК) генетической оптимизации на основе системы динамического моделирования ситуаций (СДМС) BPsim.MAS и системы технико-экономического проектирования (ТЭП) BPsim.MSN. СДМС BPsim.MAS поддерживает построение мультиагентных имитационных моделей с помощью графической нотации процессов преобразования ресурсов. Система ТЭП BPsim.MSN обеспечивает разработку интеллектуальных агентов поиска решения с помощью технологии проектирования визардов с использованием диаграмм последовательности на основе языка UML и языка управления базами данных Transact-SQL.
В ходе разработки ПК был спроектирован интеллектуальный агент (ИА) генетической оптимизации. Алгоритм работы ПК в ходе оптимизации решения задачи управления сложными организационно-техническими системами (ОТС) представлен на рисунке 1.
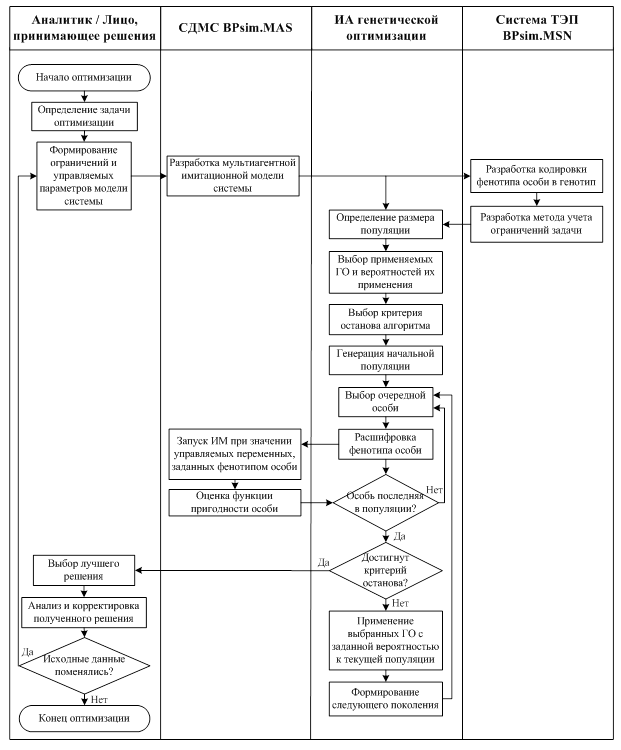
Рис. 1. Алгоритм работы программного комплекса мультиагентной генетической оптимизации
Разработанный ПК мультиагентной генетической оптимизации по сравнению с существующими ПК эволюционной оптимизации [2–3,6] обладает рядом преимуществ:
1. Интеграция имитационного, экспертного, мультиагентного, концептуального и эволюционного подходов.
2. Описание моделей системы с использованием графических нотаций: мультиагентных процессов преобразования ресурсов и языка UML.
3. Ориентация на широкий класс задач управления сложными ОТС за счет предоставления пользователю возможности настройки готового решения задачи на конкретные условия с помощью задания параметров ГА.
4. Предоставление пользователю возможности соотнесения эволюционной и имитационной моделей предметной области с помощью технологии визарда.
5. Поддержка разработки пользователем собственного способа решения задачи управления ОТС с помощью ГА на основе описания кодирования фенотипа особи в генотип.
Применение ПК мультиагентной генетической оптимизации
Рассмотрим применение разработанного программного комплекса для решения задачи планирования работ по портфелю проектов на предприятии ЗАО «Телесистемы». Целью планирования является минимизация простоя собственных отделов предприятия, а также минимизация стоимости субподрядных работ по портфелю проектов. Детальная постановка задачи приведена в [1].
В ходе разработки эволюционной модели исследуемой системы были рассмотрены различные варианты кодирования решения в особь хромосому: кодирование последовательности работ [5–6], кодирование приоритетов работ [7], кодирование правил назначения работам приоритетов [3], кодирование календарных дат начала работ [4]. В результате был выбран метод кодирования дат начала работ благодаря отсутствию избыточности при кодировании и поддержке учета временных ограничений.
Для оценки ФП решения по формуле (3) была разработана мультиагентная имитационная модель исполнения работ по портфелю проектов в среде BPsim.MAS с реализацией динамического распределения собственных и субподрядных ресурсов по работам [1]. Управляемые параметры (входные данные) модели представляют собой даты начал операций проектов портфеля. Для ГА в ходе работы ИА генетической оптимизации были заданы следующие параметры: 1) размер популяции – 10 особей; 2) размер особи – 175 ген (5 ген на кодирование каждой из 35 рассматриваемых операций портфеля); 3) применяемые ГО – репродукция на основе рулетки, пятиточечный кроссинговер, пятиточечная мутация с вероятностью 10 %, инверсия с вероятностью 5% [3]; 4) критерий останова алгоритма – смена 10 поколений; 5) генерация случайной начальной популяции.
В результате работы ПК генетической оптимизации была получена зависимость значений ФП особей популяции и значений ЦФ задачи от смены поколений. На рис. 2 слева представлено изменение минимального значения ЦФ задачи (1) при генетической оптимизации, а справа – изменение максимального значения ФП особи ГА (3) в ходе его выполнения. Как следует из графиков, наилучшее решение было достигнуто в 7 поколении.
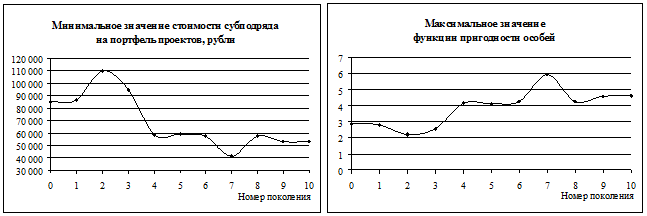
Рис. 2. Зависимость ЦФ задачи планирования и ФП особи ГА от смены поколений
Задача планирования проектных работ была решена также разработанным эвристико-имитационным методом на основе анализа выходных параметров имитационной модели деятельности предприятия [1]. Гистограммы целевых функций (1) и (2) решений задачи, полученных с помощью рассмотренных методов, приведены на рис. 3 в сравнении с ЦФ начального плана работ, интуитивно составленного ЛПР с учетом имеющегося опыта и квалификации.
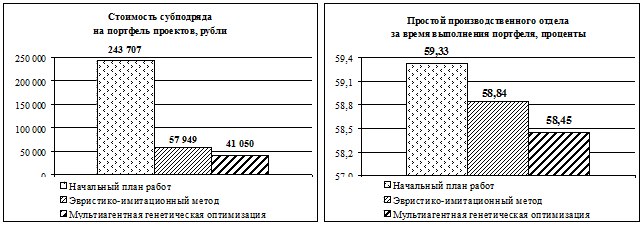
Рис. 3. Изменение значений целевых функций задачи в зависимости от метода решения
В результате анализа решений задачи планирования, найденных различными методами, был сделан вывод о наиболее эффективной работе метода мультиагентной генетической оптимизации. Применение данного метода позволило снизить на 30 % стоимость субподрядных работ по портфелю проектов, на 1,5 % простой производственного отдела в течение полугода по сравнению с предложенным эвристико-имитационным методом, а также снизить стоимость субподрядных работ по портфелю проектов в 6 раз по сравнению с начальным решением.
Заключение
Применение при решении задачи планирования проектных работ генетической оптимизации на основе интеграции имитационного и эволюционного моделирования позволяет повысить эффективность найденного решения за счет учета в ИМ динамического характера распределения ресурсов по работам и проведения генетическим алгоритмом направленного поиска в пространстве решений. Экономический эффект от использования разработанного ПК генетической оптимизации при решении задачи планирования на предприятии ЗАО «Телесистемы» составил 405 000 рублей в год, что на 9 % выше экономического эффекта от применения эвристико-имитационного метода для решения той же задачи.
Исследование проведено при финансовой поддержке молодых ученых УрФУ в рамках реализации программы развития УрФУ.Рецензенты:
Поршнев Сергей Владимирович, д.т.н., профессор, заведующий кафедрой радиоэлектроники и информационных систем, ФГАОУ ВПО “Уральский федеральный университет им. первого Президента России Б. Н. Ельцина”, г. Екатеринбург.
Доросинский Леонид Григорьевич, д.т.н., профессор, заведующий кафедрой Информационных технологий, ФГАОУ ВПО “Уральский федеральный университет им. первого Президента России Б. Н. Ельцина”, г. Екатеринбург.
Библиографическая ссылка
Антонова А.С., Аксенов К.А. ГЕНЕТИЧЕСКАЯ ОПТИМИЗАЦИЯ ПРИ РЕШЕНИИ ЗАДАЧИ ПЛАНИРОВАНИЯ ПРОЕКТНЫХ РАБОТ // Современные проблемы науки и образования. – 2012. – № 6. ;URL: https://science-education.ru/ru/article/view?id=7409 (дата обращения: 08.11.2024).