Разработка методов и способов управления подвижными объектами и создание на основе этих разработок систем навигации и наведения является одной из актуальных задач судовождения. Для случая движения судна между двумя точками (отхода и прихода) эта задача имеет достаточно обоснованное решение, по результатам которого созданы автоматизированные системы управления движением судов [3, 4].
Однако в тех случаях, когда судно по криволинейной траектории сближается с подвижным объектом, существует ряд нерешённых проблем, связанных, прежде всего, с обоснованием методов сближения.
Цель исследования
Теоретическое обоснование метода сближения судна, основу которого составляют исходные положения пропорциональной навигации [2], с подвижным объектом на примере сближения с локальным скоплением рыбы (косяком).
Материал исследования
По характеру связи между направлениями вектора скорости судна и линии пеленга на косяк все методы наведения можно разделить на две подгруппы:
- Методы с фиксированным направлением вектора скорости относительно линии пеленга (метод погони, метод постоянного угла упреждения).
- Методы с изменяющимся направлением вектора скорости относительно линии пеленга (метод параллельного сближения и метод пропорционального сближения).
Выбор метода наведения необходимо производить с учетом ряда требований.
- Метод наведения должен обеспечивать наименьшую кривизну траектории судна, особенно в районе точки встречи судна с подвижным объектом (косяком). При этом необходимо учитывать ограничение по минимальному радиусу циркуляции судна. Кривизна кинематической траектории в районе точки встречи влияет на величину ошибок наведения судна на косяк. Следовательно, уменьшение кривизны кинематической траектории по мере приближения судна к цели - одно из существенных требований к методу наведения.
- Метод наведения должен обеспечивать выход судна на косяк во всем возможном диапазоне скоростей и направлений движения косяка.
- Метод наведения должен обеспечивать требуемую точность сближения судна с косяком в различных гидрометеорологических и промысловых условиях.
- Метод наведения должен быть достаточно простым в смысле его реализации.
Для вывода уравнений, учитывающих перечисленные требования к методу наведения и описывающих кинематику сближения судна с подвижным объектом, рассмотрим относительное движение двух точек A и B в соответствии с рисунком 1 [5].

Рис. 1. Кинематические параметры облова косяка
Точка B (косяк рыбы) является преследуемой, точка A (судно) - преследующей. Для вывода уравнений движения точки A относительно точки B выберем полярную систему координат с радиус-вектором D (AB) и полярным углом h. Разложим сложное движение точки A относительно точки B на два простых: поступательное по линии AB и вращательное по линии перпендикулярной к AB. Для этого спроектируем векторы скорости судна Vs и косяка Vf на линию AB и перпендикулярное к ней направление. В результате получим следующую систему дифференциальных уравнений
|
|
|
Отсюда
|
|
(1)
(2) |
где  - скорость изменения дистанции между судном и косяком; η - угол поворота линии визирования (линии пеленга) АВ (отрицательное значение - пеленг на косяк П); γ - угол упреждения (отрицательное значение - курсовой угол на косяк КУ); D - дистанция между судном и косяком[1];
- скорость изменения дистанции между судном и косяком; η - угол поворота линии визирования (линии пеленга) АВ (отрицательное значение - пеленг на косяк П); γ - угол упреждения (отрицательное значение - курсовой угол на косяк КУ); D - дистанция между судном и косяком[1]; ![]() - скорость поворота линии визирования (отрицательное значение - скорость изменения пеленга на косяк
- скорость поворота линии визирования (отрицательное значение - скорость изменения пеленга на косяк ![]() ).
).
Примечание. Приведённые пояснения значений символов в уравнениях (1) и (2) приняты в пропорциональной навигации [2]. В скобках дается их аналогия в морской навигации [1].
Добавим к уравнениям (1) и (2) геометрическое соотношение
|
|
(3) |
где ψ - угол между вектором скорости судна Vs и осью Y (Nи), задающей неподвижное направление (см. рис. 1).
Тогда, полагая Vf известной по величине и направлению, а скорость Vs неизменной по величине, можно рассматривать систему (1) - (3) как исходную для определения относительного движения точки B. Однако эта система уравнений не замкнута: в трёх уравнениях четыре неизвестных D, η, ψ, γ. Чтобы замкнуть систему, следует задать закон изменения направления скорости судна Vs.
Это можно осуществить следующими способами:
- Направить вектор скорости судна по линии пеленга, т. е. принять g = 0.
- Положить угол упреждения равным постоянной величине, g = const.
- В процессе движения угол поворота линии визирования держать постоянным, h = const.
В результате в первом случае получим способ сближения по кривой погони, во втором - с постоянным углом упреждения, в третьем - параллельного сближения.
Обобщением этих трёх способов сближения является пропорциональная навигация. Закон пропорциональной навигации связывает угловую скорость поворота линии визирования с угловой скоростью вращения вектора скорости соотношением
|
|
(4) |
где коэффициент b называется навигационной постоянной.
Система уравнений (1) - (4) определяет кинематику точки B (судна) при пропорциональной навигации.
Перейдём от значений, принятых в пропорциональной навигации, к значениям в морской навигации. Тогда уравнения (1), (2) можно записать в виде:
|
|
(5)
(6) |
Если считать, что элементы движения судна и косяка известны, то в уравнениях (5), (6) неизвестными величинами являются D, П и КУ. Следовательно, эти уравнения не определяют однозначно траекторию движения судна.
Чтобы однозначно задать требуемую траекторию, необходимо к (5), (6) добавить ещё одно уравнение, связывающее величины П и КУ (как правило, наведение судна на косяк осуществляется по направлению, поэтому D можно исключить). В общем виде это уравнение можно написать как
|
|
(7) |
Вид функции (7) определяет метод наведения судна на косяк. Для задания этой функции обратимся к закону пропорциональной навигации (4), который применительно к рассматриваемой задаче говорит о том, что в течение всего времени сближения судна с косяком угловая скорость поворота вектора скорости судна должна оставаться пропорциональной угловой скорости линии пеленга на косяк.
При соблюдении основного требования к методу наведения можно предположить, что при сближении судна с косяком угол дрейфа равен нулю, т. е. вектор скорости судна направлен вдоль диаметральной плоскости. Тогда уравнение метода сближения будет иметь следующий вид:
|
|
(8) |
где ![]() - скорость изменения курса судна; b - коэффициент пропорциональности (навигационная постоянная).
- скорость изменения курса судна; b - коэффициент пропорциональности (навигационная постоянная).
Для реализации метода пропорционального сближения необходимо в каждый момент времени измерять угловую скорость линии пеленга на косяк и сравнивать ее с угловой скоростью вращения вектора скорости судна.
Ошибка наведения определится как разность:
|
|
|
Для вывода уравнений, описывающих движение судна при наведении по методу пропорционального сближения, проинтегрируем уравнение (8). В результате получим:
|
|
(9) |
где C - постоянная интегрирования рассчитывается как
|
|
|
Тогда, с учётом того, что КУ = П - Kс, решая совместно уравнения (5), (6) и (9), получим уравнения кинематической траектории судна, наводимого на косяк методом пропорционального сближения:
|
|
(10)
(11) |
Результаты исследования
Полученные уравнения (10), (11) описывают кинематическую траекторию судна, наводимого на косяк или другой подвижный объект методом пропорционального сближения. Для наглядности рассмотрим графический способ построения этой траектории.
После решения уравнений (10) и (11) относительно неизвестных D и П из точек К0, К1 и т. д., расположенных на линии движения косяка и соответствующих заданным моментам времени, откладываются обратные значения рассчитанных пеленгов П и по направлению этих пеленгов проводятся прямые линии в соответствии с рисунком 2.
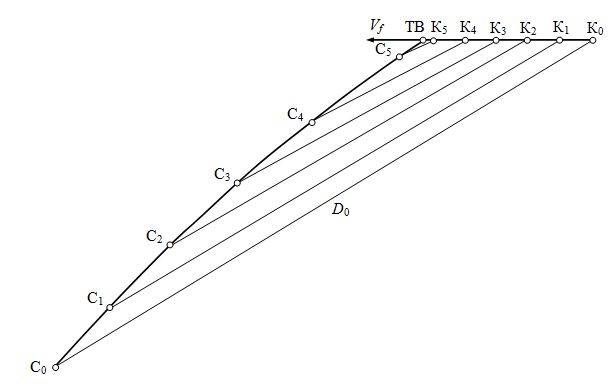
Рис. 2. Графическое построение кинематической траектории судна при методе пропорционального сближения
По этим прямым от точек местоположения косяка откладываются рассчитанные расстояния Di и ставятся точки местоположения судна С0, С1 и т. д.. Линия, соединяющая полученные точки, является кинематической траекторией движения судна при сближении с косяком (или с другим подвижным объектом) методом пропорциональной навигации. Точка пересечения этой траектории с траекторией движения косяка ТВ есть точка выхода судна на косяк.
Заключение
Метод пропорционального сближения обеспечивает возможность выхода на косяк навстречу и вдогон. Причем с точки зрения кривизны траектории и точности наведения условия сближения, вдогон более благоприятны, чем навстречу.
Таким образом, описанный метод, основу которого составляют исходные положения пропорциональной навигации, может использоваться как метод наведения судна на подвижный объект для сближения с ним.
Этот метод можно использовать при реализации технических решений по управлению судном для разработки математической модели движения судна по криволинейной траектории, алгоритмического и программного обеспечения автоматизированной системы навигации и наведения судна на подвижный объект при сближении с ним.
Рецензенты:
- Лентарёв Александр Андреевич, д.т.н., профессор, профессор кафедры судовождения ФБОУ ВПО «Морской государственный университет имени адмирала Г. И. Невельского», г. Владивосток.
- Завьялов Виктор Валентинович, д.т.н., профессор, профессор кафедры технических средств судовождения ФБОУ ВПО «Морской государственный университет имени адмирала Г. И. Невельского», г. Владивосток.
[1] Здесь и далее под дистанцией D следует понимать проекцию на плоскость горизонта наклонной дистанции Dн, зависимость между которыми определяется формулой D = Dнcosx, где x - угол наклона вибратора гидроакустической станции к плоскости горизонта.
Библиографическая ссылка
Фадюшин С.Г. СБЛИЖЕНИЕ СУДНА С ПОДВИЖНЫМ ОБЪЕКТОМ МЕТОДОМ ПРОПОРЦИОНАЛЬНОЙ НАВИГАЦИИ // Современные проблемы науки и образования. 2012. № 4. ;URL: https://science-education.ru/ru/article/view?id=6711 (дата обращения: 10.04.2025).




